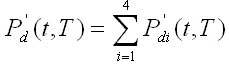|
Background
|
Courtesy of: | Ontronic Electronic Fuel Injection |
 "Decay heat is the principal reason of safety concern in Light Water Reactors (LWR)" |
||
New: A translation by Alyona Lompar in the Ukranian language is available here !
Decay heat is the heat
produced by the decay of radioactive fission products after a nuclear reactor
has been shut down. Decay heat
is the principal reason of safety concern in Light Water Reactors (LWR). It is
the source of 60% of radioactive release risk worldwide.
In a nuclear reactor, the fission of heavy atoms such as isotopes of uranium and plutonium results in the formation of highly radioactive fission products. These fission products radioactively decay at a rate determined by the amount and the type of radioactive nuclides present. Some radioactive atoms will decay while the reactor is operating and the energy released by their decay will be removed from the core along with the heat produced by the fission process. All radioactive materials that remain in the reactor at the time it is shut down and the fission process halted will continue to decay and release a significant amount of thermal energy.
The amount of radioactive materials present in the reactor at the time of shutdown is dependent on the power levels at which the reactor operated and the amount of time spent at those power levels. The amount of decay heat is very significant; a nuclear reactor operated at full power for 3 or 4 days prior to shut down has much higher decay heat generation than a reactor operated at low power for the same period.
Typically, the amount of decay heat that will be present in the reactor immediately following shutdown will be roughly 7% of the power level that the reactor operated at prior shutdown. A reactor operating at 3600 MW will produce 252 MW of decay heat immediately after shutdown; this demonstrates the importance of decay heat if no cooling is present. The amount of decay heat produced in the reactor will exponentially decrease as more and more of the radioactive material decays to some stable forms. Decay heat may decrease to about 2% of the pre-shutdown power level within the first hour after shutdown and to 1% within the first day. Decay heat will continue to decrease, but it will decrease at a much slower rate. Decay heat will be significant weeks and even months after the reactor is shut down. Failing to cool the reactor after shutdown results in core heatup and possibly core meltdown (i.e. Three Mile Island 2).
Moreover, radioactive isotopes will eventually decay to stable material. However, while they are decaying, they emit radiation (α, β-, β+ and γ). Some isotopes decay in hours or even minutes, but other decay very slowly. Those high-level wastes are hazardous to humans and other life forms because of their high radiation levels. For example, ten years after removal from a reactor, the surface dose rate for a typical spent fuel assembly exceeds 10’000 rem/hour, whereas a fatal whole-body dose for humans is about 500 rem (if received all at one time). Furthermore, if constituents of these high-level wastes were to get into ground water or rivers, they could enter into food chains. Although the dose produced through this indirect exposure is much smaller than a direct exposure dose, there is a greater potential for a larger population to be exposed. That’s the reason why nuclear wastes must be stored in a way that provides adequate protection for very long times.
The decay heat power comes mainly from five sources:
Heat production due to delayed neutron induced fission or spontaneous fission is usually neglected. Activation of light elements in structural materials plays a role only in special circumstances, and is usually excluded from decay heat analyses.
To summarize, after the shutdown of a nuclear reactor, the radioactive decay of fission products, actinides and activation products produces heat that have be removed from the system.
In nuclear power plant, decay heat removal is achieved by Emergency Core Cooling Systems and heat exchangers. Those highly redundant systems are designed to provide sufficient amount of makeup water for several days without operator intervention.
It is of high importance to precisely know the amount of decay heat in order to assess core and containment cooling strategy during abnormal event.
ANS standard for decay heat calculation
Data from several experiments were examined in the 1960s to provide an accurate basis for predicting fission product decay heat power. In 1971, the results were adopted by the American Nuclear Society (ANS) to assemble the first decay heat standard (ANS-5.1/N18.6). The ANS-5.1/N18.6 draft later updated to the ANS-5.1-1973 draft standard contained a single curve to represent all uranium-fuelled reactors.
New measurements in the seventies led to a new compilation that resulted in the adopted standard in 1979 (ANS-5.1-1979). The standard was developed to fulfil a need for evaluations of fission reactor performance dependent upon knowledge of decay-heat power in the fuel elements. Since the approval of the standard, new measurements of decay heat have been published. In addition, improved nuclear data bases have resulted in more precise summation calculations of decay heat. The latest version of the standard is ANS-5.1-1994 (Current Standard, Revision of ANSI/ANS-5.1-1979;R1985).
The ANS-5.1 standard provides bases for determining the shutdown decay heat power and its uncertainty following shutdown of Light Water Reactors (LWR). The information in this standard can be used in the design, performance evaluation, and assessment of the safety of LWRs. This standard can be used as the basis of determining fission product decay heat power.
The ANS-5.1 standard for decay heat generation in nuclear power plants provides a simplified mean of estimating nuclear fuel cooling requirements that can be readily programmed into computer codes used to predict plant performance. The ANS-5.1 standard models the energy release from the fission products of 235U, 238U and 239Pu using a summation of exponential terms with empirical constants. Corrections are provided to account for energy release from the decay of 239U and 239Np and for the neutron activation of stable fission products. Although the empirical constants are built into the standards, certain data inputs are left to the discretion of the user. These options permit accounting for differences in power history, initial fuel enrichment and neutron flux level.
Decay heat power from other actinides and activation products in structural materials, and fission power from delayed neutron-induced fission, are not included in this standard.
The standard methods of evaluating decay heat described herein are applicable to LWRs containing 235U as the initial major fissile material and 238U as the fertile material. The contributions from 235U, 238U, 239Pu and 241Pu are treated explicitly. Standard fission-product decay heat power representations are provided in tabular form for thermal reactor neutron spectrum fission of 235U, 239Pu and 241Pu, and fast fission of 238U, at various times after shutdown following two limiting reactor operating periods, one for a fission pulse and one for a reactor operated at a constant fission rate for an infinite period of time and then instantaneously shut down.
These standard representations do not account for neutron capture by fission products. Uncertainties are provided for each shutdown time for each of the tabulations. Methods are prescribed for obtaining the total fission-product decay heat power and the associated uncertainty for finite operating times from either the pulse or infinite operation representations. A method is prescribed to account for the effect of neutron capture in fission products for shutdown times less than 104 seconds; it uses a multiplying factor that depends upon reactor operating time, total fission per initial fissile atom, and the time after shutdown. The upper bound for this factor is also prescribed for shutdown times up to 1010sec. The user has the option of computing and justifying the neutron capture correction
The data on fission product decay heat power are presented in two ways in this standard. The first is fi (t), which represents decay heat power per fission following an instantaneous pulse of a significant number of fission events.
The second method of presentation is Fi (t,∞), the decay heat power from fission products produced at a constant rate over an infinitely long operating period without neutron absorption in the fission products.
Methods are prescribed for obtaining the decay heat power for an arbitrary reactor power history without neutron capture in fission products. Neutron capture in fission products has a small effect upon decay heat power for 0<t<104 sec, and is treated as a correcting factor . The total decay power is given by: Pd(t,T) = P'd(t,T)G(t) where Pd(t,T) corresponds to the total fission product decay heat power at t sec after shutdown for an operating time T sec. We have:
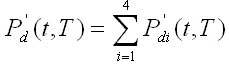
and i = 1, 2, 3 and 4 represent 235U thermal, 239Pu thermal, 238U fast and 241Pu, respectively.
Neglecting the neutron capture effect, the beta and gamma decay heat produced per fission event is only a function of the decay time. Let b(t) and g(t) be these decay heat sources, respectively. The total decay heat function per fission event f(t) is simply the sum of b(t) and g(t). If a fissile nuclide is being irradiated for a time I with a constant fission rate, the decay heat at a time t’ following the irradiation can be calculated by regarding the irradiation as series of fission bursts as shown below.
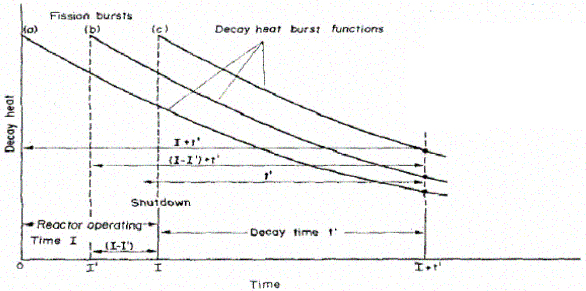
For each fission burst, the contribution to the beta decay
power per unit fission rate equals b(t)dt. Then the total beta decay
power at decay time t’ normalized per unit fission rate is expressed
by:
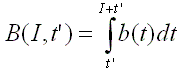
A similar expression is found for the gamma decay heat G (I, t’) and the total decay heat F (I, t’). If the irradiation time is small compared with the decay time t’, the function B (I, t’), and similarly for G (I, t’) and F (I, t’), can be approximated by:
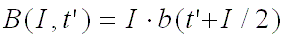
This simply states that for a short irradiation time and a long decay time, the decay heat can be approximated by the burst function evaluated at time t’+I/2. The function B (I, t’) can be written as a difference of two integrals:
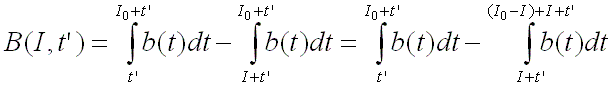
By taking the limit of I0 to infinity, the function B(I,t’) can be written as the difference of two terms at infinite radiation:
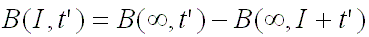
This is the infinite state governing equation for decay heat calculation.
Similar formula applies for the gamma decay power and the total decay power.
The functions b(t’), g(t’) and f(t’) are expressed in units of (MeV/second) and the corresponding integral quantities B(I,t’), G(I,t’) and F(I,t’) are expressed in units of (MeV/fission) per (fission/second), i.e. effectively in units of (MeV/second).
The decay heat is then summed up for each batch and each power segment using the following formula:
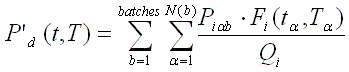
Where:
N (b) is the number periods for batch.
b and a are index specifying an operating period at constant
power level.
Qi
is the total recoverable energy (fission +decay) associated with one fission of
nuclide i, expressed in [MeV/fission]
In order to efficiently use the ANS-5.1-94 standard for nuclear power plant application, an interactive C++ software has been developed: DECANS V1.2. It calculates decay heat power based on the ANS-5.1-94 standard. It has been developed as a “stand-alone” program and has been implemented into the MELSIM / MELCOR environment.
DECANS V1.2 has been useful to define core configuration inputs and is suitable for PSA Level 2 applications, independent analysis and real-time accident management.
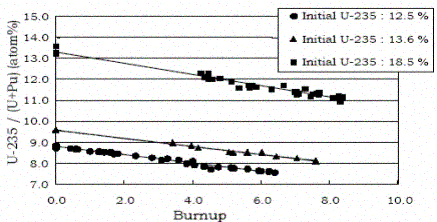
DECANS V1.2 automatically evaluates the fractional fission contribution of each fissile isotope (235U, 238U, 239Pu and 241Pu) based on the fuel burnup using published fractional contribution curves for LWRs (see example in below).
The most important part is to define the complete core history. The first operation is to define the number of batches in the core. Each batch is divided into several power segments, i.e. the different power levels of batch’s life. As an example, a 4 segments batch power history is presented below:
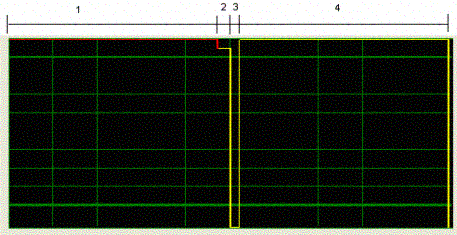
In general, there are three segments for each operating year: in the case shown above the first segment corresponds to 330 days of full power operating time at 720 MW, the second to 20 days at 684 MW for reactor coastdown (95% of the rated thermal power), and the last to 15 days of outage with no power. The second segment corresponds to a period when the power is decreased progressively until 90% of full power before normal outage shutdown. In real conditions, the decrease of power is approximately linear.
After having defined the power segments of each batch, their operating time and power levels are defined. All segments are defined in this way.
The batch mass is also needed since the burnup depends on the mass of uranium oxide. For each power segment, DECANS integrates the batch power in order to determine the burnup conditions after an operating time t*. Thanks to the curves representing the relative rate fraction of the nuclides as functions of the burnup, it is possible to know the total decay heat generated t* seconds after the containment isolation for each batch, using the ANS standard.
Finally, the decay heat curve as a function of time can be calculated. There is one curve for each batch which are then summed up to get the overall reactor decay heat curve.
The following screen snapshots of DECANS present the power history for a batch that has been loaded 3 years ago and has therefore a total of 3 irradiation periods with 7 power segments:
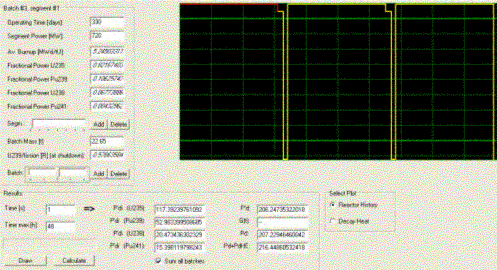
On the screen snapshots, the data calculated by DECANS are in italics, the others are user input (operating time, segment power and batch mass).
The decay power (uncorrected for neutron capture) is then calculated by DECANS with respect of each batch and each irradiation periods using the ANS standard:
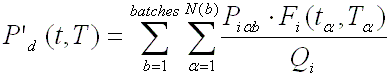
Where: N (b) is
the number periods for batch.
b and a are index specifying an operating period at constant
power level.
Qi
is the total recoverable energy (fission +decay) associated with one fission of
nuclide i, expressed in [MeV/fission]
Fi (t,T) is the decay power t seconds after an operating
period of T seconds at constant fission rate of nuclide i in the absence of any
neutron capture in the fission products,
expressed in [MeV / fission].
Two possibilities have been investigated in order to take the neutron capture effect in consideration:
The first one, as suggested in the ANS-5.1, uses the following correlation formula for shutdown time t<10’000 sec:
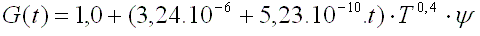
where y is the number of fissions per initial fissile atom and may be determined from the initial U235 enrichment and total burnup as follow:
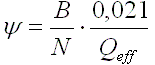
where B is the burnup and N the initial enrichment in percent
For time above 10’000 sec, a pre-calculated table (as given in the ANS standard) is used to evaluate the G values as a function of shutdown time t.
The second method uses the pre-calculated table from the beginning up to the end of the calculation.
The advantage of the first option resides in its higher accuracy. However, the switch between correlation and the table causes a discontinuity at 10’000 sec after transient initiation (see below):
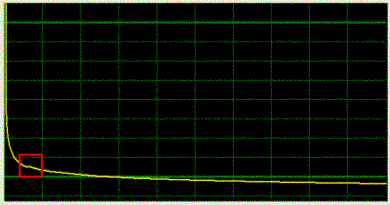
The following DECANS box allows choosing between the two options:
In accordance to the ANS standard, contribution from U239 and Np239 has been credited in DECANS using the following expressions:
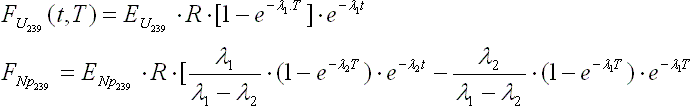
Where: EU239
and ENp239 are
the average recoverable energy from the decay of U239
and Np239 and are
equal to 0.474 MeV and 0.419 MeV respectively.
l1 and l2
are the decay constants (4.91.10-4
and 3.41.10-6 sec-1).
R is the conversion factor. It represents the number of U239
atoms produced per total fission events, evaluated at the reactor composition at
the time of shutdown.
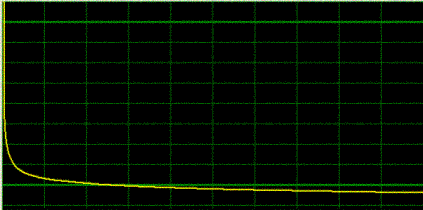
A final decay heat as generated by DECANS is shown below. The curve can then be exported to MS EXCEL using the export function.
2004-2006, Olivier Nusbaumer